Imagine como seria buscar um número em um catálogo telefônico se os nomes das pessoas não estivessem listados em ordem alfabética? Seria muito complicado. A ordenação ou classificação de registros consiste em organizá-los em ordem crescente ou decrescente e assim facilitar a recuperação desses dados. A ordenação tem como objetivo facilitar as buscas e pesquisas de ocorrências de determinado elemento em um conjunto ordenado.
Como preza a estratégia algorítmica: “Primeiro coloque os números em ordem. Depois decidimos o que fazer.”
Na computação existe uma série de algoritmos que utilizam diferentes técnicas de ordenação para organizar um conjunto de dados, eles são conhecidos como Métodos de Ordenação ou Algoritmos de Ordenação. Vamos conhecer um pouco mais sobre eles.
Os métodos de ordenação se classificam em:
-
Ordenação Interna: onde todos os elementos a serem ordenados cabem na memória principal e qualquer registro pode ser imediatamente acessado.
-
Ordenação Externa: onde os elementos a serem ordenados não cabem na memória principal e os registros são acessados sequencialmente ou em grandes blocos.
Hoje veremos apenas os métodos de ordenação interna.
Dentro da ordenação interna temos os Métodos Simples e os Métodos Eficientes:
Curso C Básico
Conhecer o cursoMétodos Simples
Os métodos simples são adequados para pequenos vetores, são programas pequenos e fáceis de entender. Possuem complexidade C(n) = O(n²), ou seja, requerem O(n²) comparações. Exemplos: Insertion Sort, Selection Sort, Bubble Sort, Comb Sort.
Dica: Veja uma breve introdução à análise de algoritmos
Nos algoritmos de ordenação as medidas de complexidade relevantes são:
- Número de comparações
C(n)entre chaves. - Número de movimentações
M(n)dos registros dos vetores.
Onde n é o número de registros.
Insertion Sort
Insertion Sort ou ordenação por inserção é o método que percorre um vetor de elementos da esquerda para a direita e à medida que avança vai ordenando os elementos à esquerda. Possui complexidade C(n) = O(n) no melhor caso e C(n) = O(n²) no caso médio e pior caso. É considerado um método de ordenação estável.
Um método de ordenação é estável se a ordem relativa dos itens iguais não se altera durante a ordenação.
O funcionamento do algoritmo é bem simples: consiste em cada passo a partir do segundo elemento selecionar o próximo item da sequência e colocá-lo no local apropriado de acordo com o critério de ordenação.


(Imagens: Wikipedia.org)
Vejamos a implementação:
void insercao (int vet, int tam){
int i, j, x;
for (i=2; i<=tam; i++){
x = vet[i];
j=i-1;
vet[0] = x;
while (x < vet[j]){
vet[j+1] = vet[j];
j--;
}
vet[j+1] = x;
}
Para compreender melhor o funcionamento do algoritmo veja este vídeo:
Selection Sort
A ordenação por seleção ou selection sort consiste em selecionar o menor item e colocar na primeira posição, selecionar o segundo menor item e colocar na segunda posição, segue estes passos até que reste um único elemento. Para todos os casos (melhor, médio e pior caso) possui complexidade C(n) = O(n²) e não é um algoritmo estável.


(Imagens: Wikipedia.org)
Veja este vídeo para conhecer o passo a passo de execução do algoritmo:
void selecao (int vet, int tam){
int i, j, min, x;
for (i=1; i<=tam-1; i++){
min = i;
for (j=i+1; j<=tam; j++){
if (vet[j] < vet[min])
min = j;
}
x = vet[min];
vet[min] = vet[i];
vet[i] = x;
}
}
Métodos Eficientes
Os métodos eficientes são mais complexos nos detalhes, requerem um número menor de comparações. São projetados para trabalhar com uma quantidade maior de dados e possuem complexidade C(n) = O(n log n). Exemplos: Quick sort, Merge sort, Shell sort, Heap sort, Radix sort, Gnome sort, Count sort, Bucket sort, Cocktail sort, Timsort.
Quick Sort
O Algoritmo Quicksort, criado por C. A. R. Hoare em 1960, é o método de ordenação interna mais rápido que se conhece para uma ampla variedade de situações.
Provavelmente é o mais utilizado. Possui complexidade C(n) = O(n²) no pior caso e C(n) = O(n log n) no melhor e médio caso e não é um algoritmo estável.
É um algoritmo de comparação que emprega a estratégia de “divisão e conquista”. A ideia básica é dividir o problema de ordenar um conjunto com n itens em dois problemas menores. Os problemas menores são ordenados independentemente e os resultados são combinados para produzir a solução final.
Basicamente a operação do algoritmo pode ser resumida na seguinte estratégia: divide sua lista de entrada em duas sub-listas a partir de um pivô, para em seguida realizar o mesmo procedimento nas duas listas menores até uma lista unitária.
Funcionamento do algoritmo:
- Escolhe um elemento da lista chamado pivô.
- Reorganiza a lista de forma que os elementos menores que o pivô fiquem de um lado, e os maiores fiquem de outro. Esta operação é chamada de “particionamento”.
- Recursivamente ordena a sub-lista abaixo e acima do pivô.
Dica: Conheça um pouco sobre algoritmos recursivos

(Imagem: Wikipedia.org)
Veja este vídeo para conhecer o passo a passo de execução do algoritmo:
void quick(int vet[], int esq, int dir){
int pivo = esq, i,ch,j;
for(i=esq+1;i<=dir;i++){
j = i;
if(vet[j] < vet[pivo]){
ch = vet[j];
while(j > pivo){
vet[j] = vet[j-1];
j--;
}
vet[j] = ch;
pivo++;
}
}
if(pivo-1 >= esq){
quick(vet,esq,pivo-1);
}
if(pivo+1 <= dir){
quick(vet,pivo+1,dir);
}
}
A principal desvantagem deste método é que ele possui uma implementação difícil e delicada, um pequeno engano pode gerar efeitos inesperados para determinadas entradas de dados.
Mergesort
Criado em 1945 pelo matemático americano John Von Neumann o Mergesort é um exemplo de algoritmo de ordenação que faz uso da estratégia “dividir para conquistar” para resolver problemas. É um método estável e possui complexidade C(n) = O(n log n) para todos os casos.
Esse algoritmo divide o problema em pedaços menores, resolve cada pedaço e depois junta (merge) os resultados. O vetor será dividido em duas partes iguais, que serão cada uma divididas em duas partes, e assim até ficar um ou dois elementos cuja ordenação é trivial.
Para juntar as partes ordenadas os dois elementos de cada parte são separados e o menor deles é selecionado e retirado de sua parte. Em seguida os menores entre os restantes são comparados e assim se prossegue até juntar as partes.


(Imagens: Wikipedia.org)
Veja o vídeo para conhecer o passo a passo da execução do algoritmo:
void mergeSort(int *vetor, int posicaoInicio, int posicaoFim) {
int i, j, k, metadeTamanho, *vetorTemp;
if(posicaoInicio == posicaoFim) return;
metadeTamanho = (posicaoInicio + posicaoFim ) / 2;
mergeSort(vetor, posicaoInicio, metadeTamanho);
mergeSort(vetor, metadeTamanho + 1, posicaoFim);
i = posicaoInicio;
j = metadeTamanho + 1;
k = 0;
vetorTemp = (int *) malloc(sizeof(int) * (posicaoFim - posicaoInicio + 1));
while(i < metadeTamanho + 1 || j < posicaoFim + 1) {
if (i == metadeTamanho + 1 ) {
vetorTemp[k] = vetor[j];
j++;
k++;
}
else {
if (j == posicaoFim + 1) {
vetorTemp[k] = vetor[i];
i++;
k++;
}
else {
if (vetor[i] < vetor[j]) {
vetorTemp[k] = vetor[i];
i++;
k++;
}
else {
vetorTemp[k] = vetor[j];
j++;
k++;
}
}
}
}
for(i = posicaoInicio; i <= posicaoFim; i++) {
vetor[i] = vetorTemp[i - posicaoInicio];
}
free(vetorTemp);
}
Shell Sort
Criado por Donald Shell em 1959, o método Shell Sort é uma extensão do algoritmo de ordenação por inserção. Ele permite a troca de registros distantes um do outro, diferente do algoritmo de ordenação por inserção que possui a troca de itens adjacentes para determinar o ponto de inserção. A complexidade do algoritmo é desconhecida, ninguém ainda foi capaz de encontrar uma fórmula fechada para sua função de complexidade e o método não é estável.
Os itens separados de h posições (itens distantes) são ordenados: o elemento na posição x é comparado e trocado (caso satisfaça a condição de ordenação) com o elemento na posição x-h. Este processo repete até h=1, quando esta condição é satisfeita o algoritmo é equivalente ao método de inserção.
A escolha do salto h pode ser qualquer sequência terminando com h=1. Um exemplo é a sequencia abaixo:
h(s) = 1, para s = 1
h(s) = 3h(s - 1) + 1, para s > 1
A sequência corresponde a 1, 4, 13, 40, 121, …
Knuth (1973) mostrou experimentalmente que esta sequencia é difícil de ser batida por mais de 20% em eficiência.
Veja o vídeo que demonstra o passo a passo da execução do algoritmo:
void shellSort(int *vet, int size) {
int i , j , value;
int gap = 1;
while(gap < size) {
gap = 3*gap+1;
}
while ( gap > 1) {
gap /= 3;
for(i = gap; i < size; i++) {
value = vet[i];
j = i - gap;
while (j >= 0 && value < vet[j]) {
vet [j + gap] = vet[j];
j -= gap;
}
vet [j + gap] = value;
}
}
}
Curso Wordpress - Personalização e Ecossistema
Conhecer o cursoConclusão
Neste artigo foi apresentado os principais métodos de ordenação com foco no conceito e funcionamento de cada um deles.
Você pode ver na tabela abaixo a comparação entre eles:
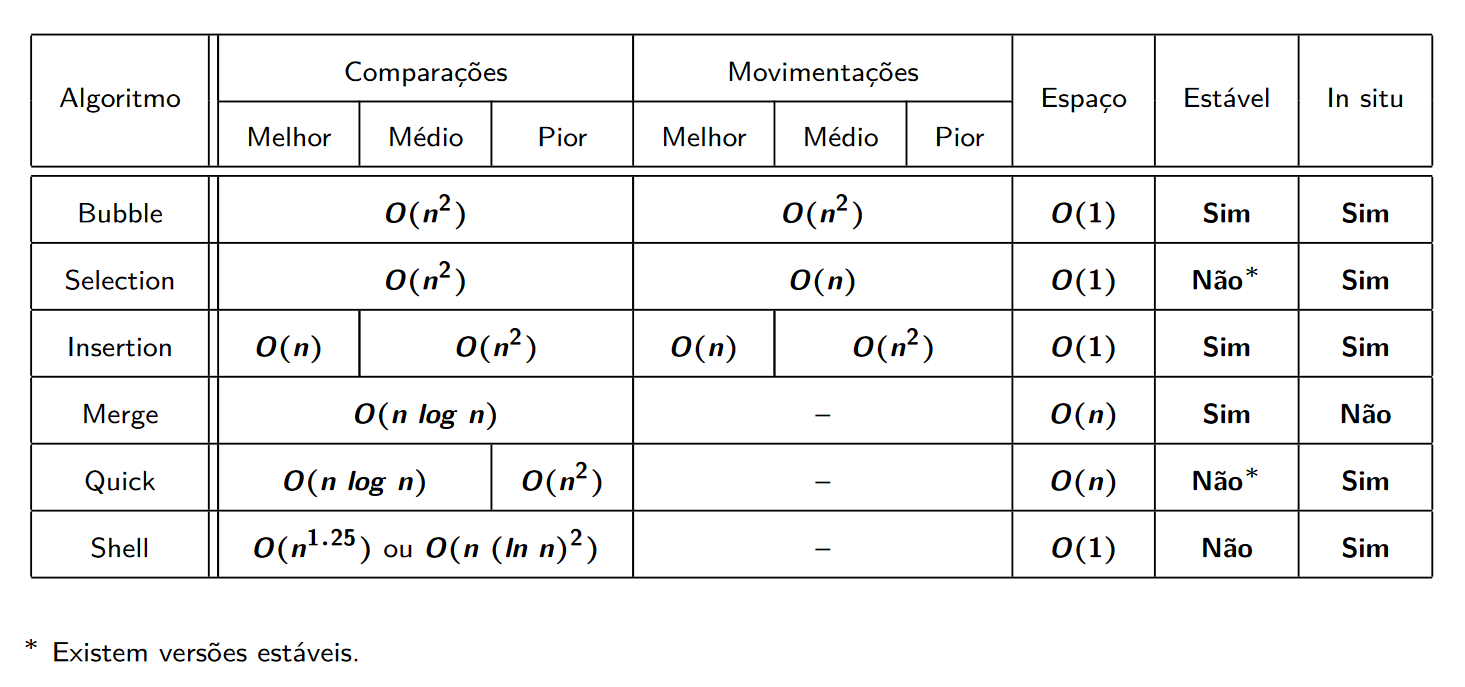
(Imagem: DECOM - UFOP)
Um abraço e até a próxima!