Resultado da busca para binario

• O que esperar do Windows Subsystem for Linux (WSL) 2

  O Windows Subsystem for Linux (WSL) 2 permite você executar qualquer binário compilado para Linux di...

• Bits, bytes e unidades de medida

  Tudo o que fazemos em um computador é processado numa sequência de zeros e uns (sistema binário). Ve...

• Função para converter HTML para PDF usando PHP e wkhtmltopdf no AWS Lambda

  Veja nesse artigo como subir uma função para o AWS Lambda para converter HTML para PDF usando wkhtml...

• Uma introdução a ASCII e Unicode

  Veja um pouco mais sobre os sistemas de codificação de caracteres ASCII e Unicode.

• Ferramenta para avaliar a complexidade de código escrito em PHP

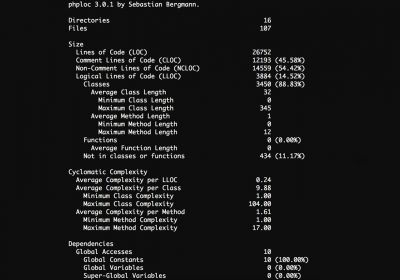
  Conheça um pouco mais sobre a phploc, ferramenta para avaliar a complexidade de código escrito em PH...

• Relatório de cobertura de testes (Code Coverage) com o PHPUnit

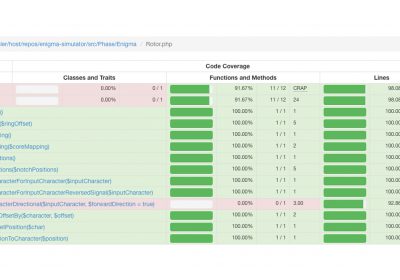
  O PHPUnit é um framework para a criação de testes unitários. Nesse artigo vamos falar sobre a geraçã...

• Guia da linguagem Go

  Nesse guia de Go você aprenderá o necessário para criar os seus primeiros softwares com a linguagem...

• Configurando ambiente de desenvolvimento Spring Boot no Linux

  Aprenda como instalar e configurar o ambiente de desenvolvimento Spring Boot no Linux

• Configurando ambiente de desenvolvimento Spring Boot no Windows

  Aprenda como instalar e configurar o ambiente de desenvolvimento Spring Boot no Windows

• O que é Windows Subsystem for Linux (WSL)?

  Nesse artigo vamos aprender o que é o Windows Subsystem for Linux (WSL), quais as suas funcionalidad...

• Binary Literals, Digit Separators e Throw Expressions no C# 7.0

  Conheça os recursos Binary Literals, Digit Separators e Throw Expressions da versão 7 do C#.

• Aplicações em tempo real com ASP.NET Core SignalR

  Aprenda como criar uma streaming api utilizando a biblioteca de aplicações em templo real, SignalR.

• JSON vs Objeto JavaScript - Qual a diferença?

  Muitas pessoas acreditam que JSON e Objeto JavaScript são a mesma coisa. Descubra a diferença.

• Como instalar a Golang e executar nosso primeiro exemplo

  Neste artigo iremos aprender como instalar a Golang nos sistemas Windows, Linux e macOS e como execu...

• O que é e como começar com Go (Golang)?

  Neste artigo vamos ter o contato inicial com a linguagem Go (Golag) e aprender um pouco sobre as sua...

• O que é NPM e como usar uma biblioteca instalada por ele

  Saiba o que é o NPM (Node Package Manager), como utilizar um pacote, framework ou biblioteca instala...

• Introdução ao Maven, aprenda como criar e gerenciar projetos Java

  Neste artigo veremos como instalar o Maven e como podemos utilizá-lo para nos auxiliar na criação e...

• O que são os 12 Factor App? – Parte 2

  No artigo anterior, foi apresentado o conceito do 12 Factor App. Nessa segunda parte, veremos mais...

• Como instalar e configurar o AWS CLI

  O AWS CLI é uma ferramenta em linha de comando capaz de gerenciar recursos na AWS. Com ela é possíve...

• Serviços gratuitos do Google Cloud Platform

  Conheça os principais serviços gratuitos do Google Cloud Platform e seus limites de uso.